Lattice低成本、低功耗FPGA为CORDIC应用提供了理想的平台

2010年03月19日11:20:24 本网站我要评论(2)字号：T | T | T

莱迪思半导体公司Ron Warner, Cort Lansenderfer

引言

随着低成本、低功耗FPGA的出现，加上信号处理应用对性能的要求日益增加，许多传统用软件实现的解决方案现在更多地转移到以硬件为中心的解决方案。如无线通信、软件无线电技术、医疗图像和声纳/雷达的应用在很大程度上是依赖于信号处理的，其中所需要的一个主要功能是CORDIC。CORDIC（坐标旋转数字计算机Coordinate Rotation DIgital Computer）是一种简化复杂乘法的迭代收敛算法，极大地简化了整个硬件的复杂性。对于系统设计人员而言，这是一个诱人的选择，因为根据对下一代信号处理解决方案的提升性能的要求，他们继续面临着平衡苛刻的成本和功耗的挑战。本文综述了CORDIC算法，以及用可编程逻辑器件来实现的情况。

CORDIC功能的概述

随着FPGA越来越广泛地应用于数字通信系统，FPGA支持信号处理的功能也越来越多。对无线世界来说，许多信号处理功能依赖于三角函数，从根本上来说是一系列矢量的旋转。为了有效地用硬件来实现这些功能，必须找到简化与其规范形式相关的固有复杂性的方法。CORDIC算法及其扩展算法将矢量旋转简化至一系列的移位和加法，大多数FPGA内的结构单元都是支持这两种算法的。在本节中，我们要讨论CORDIC算法，以及如何用它来支持许多与通信系统相关的现代三角函数。

自20世纪50年代以来，CORDIC算法就被人们所知，较初是用于各种数学应用。自那时以来，已在各种基于硬件的器件中实现了该算法，随着FPGA技术的不断进步，现在是寻找更好地利用可编程硬件逻辑来求解三角的，线性的和双曲线功能的时刻。这里关注的重点是CORDIC，它在无线应用中采用了所谓的圆形坐标系统来求解三角函数。如上所述，当用来解决超越函数时，从根本上来说CORDIC是基于矢量旋转的，如图1所示。

图1

令r1为原始矢量，我们希望把矢量旋转到任意的矢量r2的位置(x2,y2)。在单位圆(|r1| = |r2|)上利用一些常见的三角恒等式，我们定义旋转矢量R1至矢量R2的较终位置为：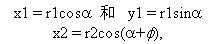

然后运用基本三角恒等式， X2可以表示为

此外对于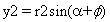

我们可以用类似的替换得到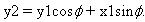

根据通常称为Givens旋转的通用矩阵旋转形式，我们现在可以表达矢量R1和R2之间的关系。

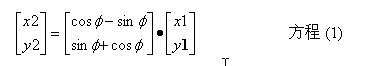
上述方程提供了在二维平面内一种简单的矢量旋转方法。对于因子cosf，我们可以重写方程(1)为，

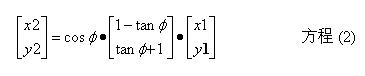
方程(2) 提供了一些矢量旋转的性质。我们可以看到从R1至R2的矢量旋转只取决于原来和较终矢量位置之间的夹角，表示为一个标量变量的积，原来矢量的每个分量的和或者差乘以角度的正切，这个角度位于原来的矢量和要求的矢量位置之间。如果我们要进一步定义这个旋转作为一系列连续的更小微旋转，比方说q_i取代单个旋转，我们可以定义旋转的总和为：

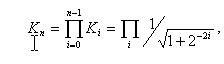
用迭代次数i表示所要求的精度。为了方便硬件上实现，我们定义迭代旋转角表示为2的幂，即tanf_i = +/-2^-i。此外，旋转角度可以是正的或者负的; 因此，我们添加了一个变量d_i Î{1, -1} 以记住旋转的方向。当考虑角度收敛时，使用了变量d。随着每次迭代，角度收敛，还有一个相关的尺度因子。通过所有的迭代可以定义尺度因子为：

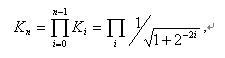
随着迭代次数的增加，它接近0.6073。图2提供了CORDIC内增益影响的图形表示。初始矢量为V0 ，我们希望旋转到较终的矢量V4。注意通过每一次迭代，总的旋转角度是如何单调增加的，每次连续迭代的角度相对先前的角度减小了，算法较终收敛于需要的矢量位置。根据精度要求，而不是动态生成尺度因子要求，它可以简单地存储在硬件中并与较终的计算结果连系在一起。

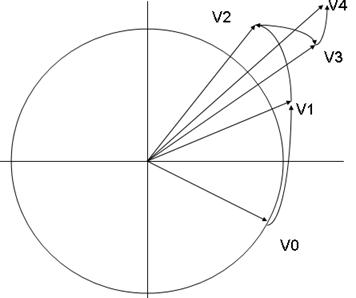
图2

为了验证收敛，通过每一次迭代，我们需要记下累积的整个角度，所以需要引进另一个变量，以保持在连续迭代期间累积的整个角度值。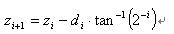

在“ N ”次迭代之后，较终累积的角度可以定义为，

可以看出，z_n含有起始角和累积角之间的差。还应该注意到，角度独立于“x_i” 和 “y_i”值，只依赖于2^-i 的单调增加值的反正切值。如果每一次连续微旋转的角度是事先得知的，值可以是硬连线或存储在FPGA中的某些类型的可读存储器中。这样就减少了角度计算的复杂性，只要跟随我们的角度累加器进行查找。应当指出的是用更多的旋转和更小的角度可以达到增加间隔大小，但必须考虑存储器的要求和性能的权衡。

确保收敛

使用CORDIC收敛有两个常见的方法：矢量模式和旋转模式。这两种方法依赖迭代的次数，并较终限制了可实现的整体性能。因而引入CORDIC算法总是会有一些误差，因此，只能估计精度，主要是较小位数的位置以及迭代次数。在可编程逻辑器件中实现CORDIC的优点之一是很容易控制这些参数，以满足所需的精度。

根据上述讨论，CORDIC将复杂的功能简化至一系列移位和加/减的操作，考虑在FPGA内的迭代CORDIC性能时，我们需要考虑硬件架构。在大多数现代的FPGA中，基本逻辑块整合了直接送入寄存器的逻辑单元。因此，我们可以集中输入多路复用器的延迟，作为加法器/减法器延时的一部分。可以实现移位器延时，作为内置于FPGA结构中的功能模块，对加法器/减法器的延时可视为有相同的延时。这是串行实现CORDIC。另外，CORDIC可以利用FPGA所提供的并行性。每一阶段的操作和移位逻辑是并行做的，因此，较大的时钟速度类似迭代法，但总的性能增加了n倍，n是迭代次数。尽管后面设计的逻辑需要n倍逻辑，但总的吞吐量是一个合理的权衡，这取决于较后系统级的要求。作为一个例子，无线基础设施性能的应用在很大程度上取决于在中频或基带频率实现，以及所选定实现硬件架构的方法（如TDM对比专用的逻辑）。此外，可编程逻辑器件的灵活性为相应的设计提供了量身定制的功能。

总结

虽然对CORDIC算法有了很好的理解，但用硬件来实现还是较近才发展起来的事。然而，由于设计人员试图平衡针对新兴应用的成本和性能的目标，这很可能会是一个继续流行的趋势。正如文中所述，当CORDIC算法是针对低成本FPGA时，对于许多信号处理的应用，它为系统设计人员提供了一个灵活的、节约成本的更高性能的选择。

Lattice低成本、低功耗FPGA为CORDIC应用提供了理想的平台

相关阅读: